Sometimes it’s a pleasure to abandon that very-cool-enterprise development, to take some book on algorithms and to solve couple of problems from it. Just to keep brain if not sharp, but at least not rusty. Also diving in some problem of that kind is the nice way to resurrect old math skills I was taught in the university.
This time I’d like to implement priority queue using d-ary heap. Don’t want to copy-paste
Wikipedia here, but priority queues are really useful data structures. The first application
that comes to mind is TOP N search results. Instead of retrieving the whole result set,
sorting it and returning first $ N $ elements it will be much faster if priority queue of size $ N $ is
used.
Sample binary heap looks like this, where all child nodes (talking about max heap here) are less or equal than their parent. (Image was taken from here http://cs.anu.edu.au/~Alistair.Rendell/Teaching/apac_comp3600/)
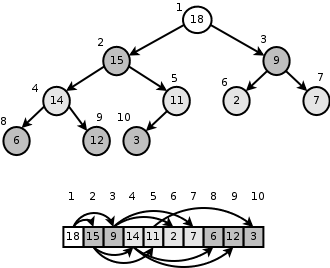
So d-ary heap. It’s just the generalization of binary heap, but each node has $ d $ children instead of 2. It’s clear that the height of the heap with $ N $ elements in it is $ \log_{d} N $.
The algorithm of extracting max element and adding new to the queue is almost the same as for binary heap, formula for getting parent-child item differs from one for binary heap.
The code sufficient to solve original problem from the book is below as long as its sample output for 4-ary heap holding 20 elements.
import math
class DAryHeap(object):
def __init__(self, d = 2):
super(DAryHeap, self).__init__()
self.d = d
self.data = []
def extract_max(self):
if not self.data:
raise Exception("No data");
m = self.data[0]
self.data[0] = self.data[self.size() - 1]
self.data.pop()
self.__heapify(0)
return m
def get_max(self):
if not self.data:
raise Exception("No data");
return self.data[0]
def increase_key(self, i, key):
if key < self.data[i]:
raise Exception("New key is less than stored")
self.data[i] = key
parent = self.__parent_index(i)
while i > 0 and self.data[parent] < self.data[i]:
self.data[parent], self.data[i] = self.data[i], self.data[parent]
i = parent
parent = self.__parent_index(i)
def insert(self, value):
self.data.append(float("-inf"))
self.increase_key(self.size() - 1, value)
def __parent_index(self, i):
return int(math.floor((i - 1) / self.d))
def __heapify(self, i):
largest = i
for j in xrange(0, self.d):
child_index = self.__get_child_index(i, j)
if child_index < self.size() - 1 and self.data[child_index] > self.data[largest]:
largest = child_index
if largest != i:
self.data[largest], self.data[i] = self.data[i], self.data[largest]
self.__heapify(largest)
def size(self):
return len(self.data)
def __get_child_index(self, i, n):
return self.d * i + n + 1
And the output
[19, 7, 11, 15, 18, 0, 4, 5, 6, 1, 8, 9, 10, 2, 12, 13, 14, 3, 16, 17]